You're reading the documentation of the v0.9. For the latest released version, please have a look at v1.1.
LOv rewriting rules in Perceval
The aim of this notebook is to rewrite a circuit using rewriting rules based on the article: LOv-Calculus: A Graphical Language for Linear Optical Quantum Circuits.
We show how to use these rewriting rules to generate unique triangular normal forms.
[1]:
import perceval as pcvl
from perceval.utils.algorithms.optimize import optimize
from perceval.utils.algorithms.norm import frobenius
import random
from perceval.rendering.circuit import DisplayConfig, SymbSkin
DisplayConfig.select_skin(SymbSkin)
This is the first rewrite rule used in this noteobok. It is the rule 37 in the article.

[2]:
pattern1=pcvl.Circuit(3, name="pattern1")//(0,pcvl.PS(pcvl.P("phi0")))//(0,pcvl.BS(theta=pcvl.P("theta1")))//(0,pcvl.PS(pcvl.P("phi2")))//(1,pcvl.PS(pcvl.P("phi1")))//(1,pcvl.BS(theta=pcvl.P("theta2")))//(0,pcvl.BS(theta=pcvl.P("theta3")))
pattern1._color = "lightgreen"
pcvl.pdisplay(pcvl.Circuit(3).add(0,pattern1,False), recursive=True)
[2]:
[3]:
rewrite1=pcvl.Circuit(3, name="rewrite")//(0,pcvl.PS(pcvl.P("beta2")))//(1,pcvl.PS(pcvl.P("beta1")))//(1,pcvl.BS(theta=pcvl.P("alpha1")))//(0,pcvl.BS(theta=pcvl.P("alpha2")))//(1,pcvl.PS(pcvl.P("beta3")))//(1,pcvl.BS(theta=pcvl.P("alpha3")))//(0,pcvl.PS(pcvl.P("beta4")))//(1,pcvl.PS(pcvl.P("beta5")))//(2,pcvl.PS(pcvl.P("beta6")))
rewrite1._color = "lightgreen"
pcvl.pdisplay(pcvl.Circuit(3).add(0,rewrite1,False), recursive=True)
[3]:
Let us implement now the rule number 1.
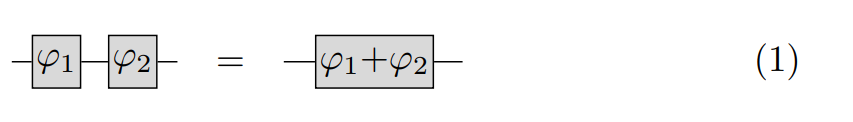
[4]:
pattern2=pcvl.Circuit(1, name="pattern2")//pcvl.PS(pcvl.P("phi1"))//pcvl.PS(pcvl.P("phi2"))
rewrite2=pcvl.Circuit(1, name="rewrite2")//pcvl.PS(pcvl.P("phi"))
[5]:
pcvl.pdisplay(pcvl.Circuit(1).add(0,pattern2,False), recursive=True)
[5]:
[6]:
pcvl.pdisplay(pcvl.Circuit(1).add(0,rewrite2,False), recursive=True)
[6]:
In fact, this rule has been directly implemented in Perceval, with the call of simplify.
[7]:
from perceval.utils.algorithms.simplification import simplify
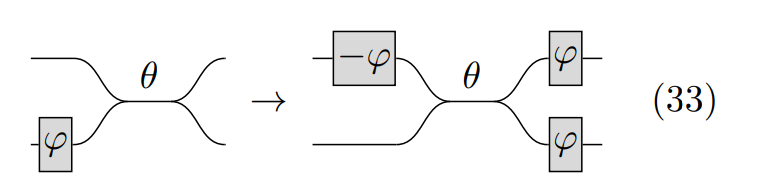
The third rule used in this notebook is the following one:
[8]:
pattern3=pcvl.Circuit(2, name="pattern3")//(1,pcvl.PS(pcvl.P("phip")))//(0,pcvl.BS(theta=pcvl.P("theta")))
pattern3._color = "pink"
pcvl.pdisplay(pcvl.Circuit(2).add(0,pattern3,False), recursive=True)
[8]:
[9]:
rewrite3=pcvl.Circuit(2, name="rewrite3")//(0,pcvl.PS(pcvl.P("phi1")))//(0,pcvl.BS(theta=pcvl.P("theta")))//(0,pcvl.PS(pcvl.P("phi2")))//(1,pcvl.PS(pcvl.P("phi3")))
rewrite3._color = "pink"
pcvl.pdisplay(pcvl.Circuit(2).add(0,rewrite3,False), recursive=True)
[9]:
And the fourth rule is the rule 38 in the article.

[10]:
pattern4=pcvl.Circuit(2, name="pattern4")//(0,pcvl.BS(theta=pcvl.P("theta1")))//(0,pcvl.PS(pcvl.P("phi1")))//(0,pcvl.BS(theta=pcvl.P("theta2")))
pattern4._color = "orange"
pcvl.pdisplay(pcvl.Circuit(2).add(0,pattern4,False), recursive=True)
[10]:
[11]:
rewrite4=pcvl.Circuit(2, name="rewrite4")//(0,pcvl.PS(pcvl.P("beta1")))//(0,pcvl.BS(theta=pcvl.P("alpha1")))//(0,pcvl.PS(pcvl.P("beta2")))//(1,pcvl.PS(pcvl.P("beta3")))
rewrite4._color = "orange"
pcvl.pdisplay(pcvl.Circuit(2).add(0,rewrite4,False), recursive=True)
[11]:
[12]:
a=pcvl.Circuit.generic_interferometer(4, lambda idx:pcvl.Circuit(2)//pcvl.PS(phi=random.random())//pcvl.BS(theta=random.random()), depth=8, shape="rectangle")
pcvl.pdisplay(a, recursive=True, render_size=0.7)
[12]:
Normalizing Circuit
[13]:
import drawsvg as draw
[14]:
reverse = []
direct=[]
def draw_frame(a):
if isinstance(a, pcvl.Circuit):
d = pcvl.pdisplay(a, recursive=True, render_size=0.6)
reverse.insert(0, d)
direct.append(d)
return d
return a
rules = [(pattern1, rewrite1, "lightgreen"), # (pattern2, rewrite2, "lightblue"),
(pattern3, rewrite3, "pink"), (pattern4, rewrite4, "orange")]
with draw.frame_animate_jupyter(draw_frame, delay=0.1) as anim:
anim.draw_frame(a)
while True:
found = False
for pattern, rewrite, color in rules:
start_pos = 0
while True:
print("matching pattern", pattern.name)
matched = a.match(pattern, browse=True, pos=start_pos)
if matched is None:
break
print("matching ok", matched.v_map)
idx = a.isolate(list(matched.pos_map.keys()), color=color)
anim.draw_frame(a)
for k, v in matched.v_map.items():
pattern.param(k).set_value(v)
v = pattern.compute_unitary(False)
print("optimizing rewrite",rewrite.name)
res = optimize(rewrite, v, frobenius, sign=-1)
print("found params with distance", res.fun)
subc = rewrite.copy()
found = True
a.replace(idx, subc, merge=False)
anim.draw_frame(a)
a.replace(idx, subc, merge=True)
pattern.reset_parameters()
rewrite.reset_parameters()
a = simplify(a)
anim.draw_frame(a)
start_pos = idx
if not found:
break
matching pattern pattern3
matching pattern pattern4
matching pattern pattern1
matching pattern pattern3
matching pattern pattern4
This representation is exactly the normal form that we wanted to obtain !
Reference
Clément, N. Heurtel, S. Mansfield, S. Perdrix, B. Valiron. LOv-Calculus: A Graphical Language for Linear Optical Quantum Circuits, 47th International Symposium on Mathematical Foundations of Computer Science MFCS, 35:1–35:16 (2022).